aximate: evolve

Robert Harlander

52056 Aachen, Germany

phone: +49-241-80-27045

fax: +49-241-80-22187

harlander(at)physik.rwth-aachen.de

Büro: 28A414, Campus Melaten

Home

Brief CV

Research

Teaching

Outreach

Conferences

– Software –

Press

collaborations:

LHC and Philosophy

DFG RTG

[Up: aximate] aximate: evolve

evolve

The default evolution from the start to the end parameters of an object is linear, i.e.

$value = $start + ($t-$t0)/($t1-$t0)*($end - $start)

where $t evolves uniformly from $t0 to $t1 during the active interval [$t0,$t1] of an object.

However, aximate allows you to modify this evolution by specifying the function of $t according to which a certain option should evolve. This is done by providing a second (referenced) hash to the object. For example, an oblique throw can be represented as:

    point({"coordinates" => [[],[]]},
    	  {"coordinates" => ['$t-50','50-2*(50-$t)**2/50']});

A jumping ball, following the path x($t) = $x0 + $b $t - 1/2 $g $t² can be aximated with a do-loop:

sub manual12 {
    my($norm,$num,$bound1,$bound2,$i,$g,$x0,$b);
    $num = 10;
    $bound1 = 0;
    $bound2 = 0;
    $norm=0;
    # make sure that the jumps fill out the full time interval:
    foreach $i (1..$num) {
      $norm += 1/sqrt(2**$i);
    }
    # the "gravitational" acceleration:
    $g = 1;
    $x0 = -98;
    for $i (1..$num) {
      # the length of the current time interval:
      $deltat = 100/$norm/sqrt(2**$i);
      $bound2 = $bound1 + $deltat;
      # with this choice of $b, it is x($bound1)=x($bound2)=$x0:
      $b = $g/2*$deltat;
      # defining empty start and end coordinates ensure that the evolution
      # is fully determined by the evolve function:
      point({"coordinates" => [[],[]],
             "interval" => [$bound1,$bound2]},
            {"coordinates" => ['0',
            $x0.'+'.$b.'*($t-'.$bound1.')-1/2*'.$g.'*($t-'.$bound1.')**2']});
      $bound1 = $bound2;
    }
}

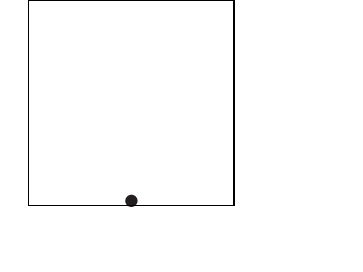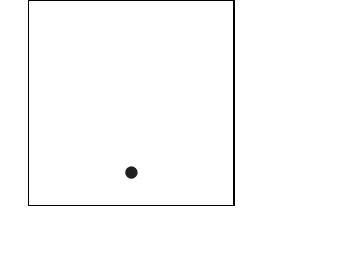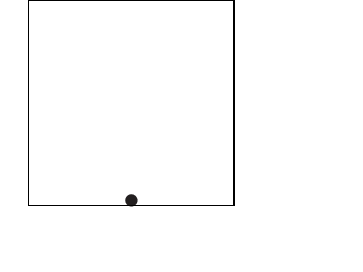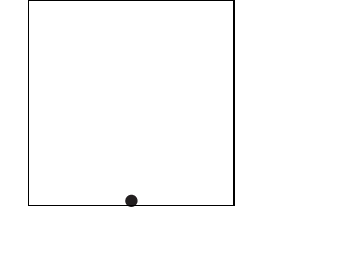
A few remarks: let us assume that f($t) is the evolution function.

If both the $start and the $end value of the evolved parameter param is given, aximate adds a linear function to the evolution such that these points are actually reached:
```
    param($t) = f($t) + $start - f(0) + $t*($end-$start-f(1)+f(0));
  
```
i.e. param(0)=$start and param(1)=$end. Note that this means that even if f($t) = const, the values will evolve linearly from the $start to the $end.
If the $end value is missing, it is assumed to be equal to the $start value, so that the evolution is circular.
If the $end value is given but empty (i.e. []), aximate sets $end=f(1), so that
```
    param($t) = f($t) + $start - f(0) + $t*(f(0)-$start);
  
```
i.e. param(0)=$start, param(1)=f(1).
If the $start value is given but empty (i.e. []), aximate sets $start=f(0), so that
```
    param($t) = f($t) + $t*($end-f(1));
  
```
i.e. param(0)=f(0), param(1)=$end.
If both the $start and the $end value is given but empty (i.e. []), the evolution function is
```
    param($t) = f($t)
  
```

It is important to note that if you want param to evolve exactly as determined by the evolution function f($t), you need to define both the start and end coordinate as empty lists. If you do not define them, aximate will use the default values which are not empty. For example,

    point({"coordinates" => [[],[]]},
	  {"coordinates" => ['50*cos(2*pi*$t)','50*sin(2*pi*$t)']});

will move a point in a circle of radius 50 around the origin, while

    point({},
	  {"coordinates" => ['50*cos(2*pi*$t)','50*sin(2*pi*$t)']});

will use the default for the coordinates parameter, which happens to be [[0,0],[0,0]]. The start and end point of the movement is thus at (0,0), so that the point will move on a circle of radius 50 around the point (-50,0).

main

aximate:evolve (Robert Harlander)