The triangular binary clock
Jörg Pretz, RWTH Aachen University
Abstract
A new idea for a binary clock is presented.
It displays the time using a triangular array of
15 lamps each representing a certain amount of time. It is shown that such a geometric,
triangular arrangement is only possible because our
system of time divisions is based on a sexagesimal system
in which the number of minutes in 12 hours
equals the factorial of a natural number (720=6!).
An interactive applet allows one to "play" with the clock.
Keywords
- binary
- clock
- time
- sexagesimal system
Subject classification
- 00 general
- 00A miscellaneous
- 00A08, 97A20 recreational mathematics
There are many ways to display the time.
For example the familiar analog display
with a dial and clock hands
or digital displays using numerals.
In addition there are binary displays which are a bit
more difficult to read.
Here a lamp lit corresponds to a certain amount of time.
The binary display presented in this article has the special feature
that the lamps are arranged in the form of a triangle.
In section 2 the clock is presented with the help of
an interactive javascript applet.
Section 3 illuminates the mathematical background
and shows that the triangluar display is only possible
because our system of time divisions is based
on a sexagesimal system rather than a decimal system.
This work is based on an article which appeared in the Journal of Recreational
Mathematics (Pretz, 2010).
The following appelt illustrates the idea.
To read off the time, you have to know that
every lamp lit in the ...
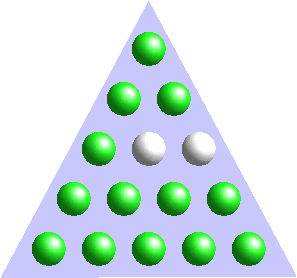
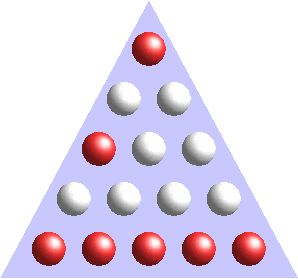
... 1st line (top line) corresponds to 6h
... 2nd line corresponds to 2h
... 3rd line corresponds to 30 min
... 4th line corresponds to 6 min
... 5th line corresponds to 1 min
green is for AM and red for PM.
You can play with the clock by using the buttons on the left.
They allow one to advance or to move back the clock in steps of one minute or one hour.
To set the time back to the present time just push the top button.
The two checkboxes allow for more help or to hide the time given in numerals
in case you would like to train yourself.
You will find out that all lamps on corresponds to 11:59 (green) or 23:59 (red).
Thus this arrangement perfectly fits for a twelve hour display.
A few examples are shown below.
 |
 |
 |
 |
| 08h 05min |
10h 59min |
18h 35min |
23h 59min |
We now come to the question why our system of time divisions allows
such a triangular display?
First note, that
the amount of time, Tn-1 , a lamp corresponds to in the (n-1)th row equals
(mn+1) times the amount, Tn, in the nth row
where mn is the number of lamps in the
nth row. Thus
Tn-1= (mn+1) Tn.
Here are two examples:
- The 3rd row has m3= 3 lamps representing 30 minutes each.
Thus for the 2nd row one finds (3+1) × 30 min = 2h.
- The 5th row has m5= 5 lamps representing 1 minute each.
Thus for the 4th row one finds (5+1) × 1 min = 6 min.
The triangular display has the special feature that
mn = n, i.e.
in the nth row there are also n lamps
This is just the condition for a triangular display.
But what does mn=n mean for the number of states
which can be represented by the display?
A row with n lamps allows one to display n+1 states,
from all lamps off to all lamps on.
(Note that in the way the display is used here,
not all of the 2n possible states are used because if a lamp is on,
also the lamps left to it are on in the same row.)
For a triangular display with n lamps
in the bottom row and the number of lamps decreasing by
one in every following row
the total number of states is thus
(n +1) × ((n-1)+1) × ((n-2)+1) ×
... × (1+1) = (n+1)!
i.e the number of states equals always a factorial of a natural number.
Now, note that our system of time measurement
is based on numbers which have many divisors,
e.g. 12=3 × 4 and 60 = 1 × 2 × 5 × 6.
For a 12 hour display with a precision of one minute the number
of states one has to display is thus
12 × 60 minutes
=1 × 2 × 3 × 4 × 5 × 6 minutes
=6! minutes
which perfectly fits in a triangular display with five rows!
Thus the whole concept works because our system of time divisions is based
on a sexagesimal system, dating back to the Babylonian (Neugebauer, 1993,
Wikipedia article "Babylonia"),
rather than a decimal system, as proposed during the French Revolution (Carrigan, 1978,
Wikipedia article "Decimal time").
References
J. Pretz (2010), A different way to read off the time -
A new idea for a binary clock,
J. of Recreational Mathematics, Vol. 35(4) 327-330, 2006,
arXiv:1006.1373v1
[math.HO]
Otto Neugebauer (1993), The Exact Sciences in
Antiquity, Barnes & Noble, New York
Richard A. Carrigan, Jr. (1978), Decimal Time,
American Scientist, 66, 305 (78)
counter
Download App
pinterest link








